53.全地連「技術e-フォーラム2005」仙台
堤体の浸透流解析における三次元的土質分布の影響に関する検討
地質基礎工業(株) 新田 邦弘
1.はじめに
河川堤防に求められる重要な機能の一つに、洪水時の浸透破壊に対する安全性があり、その評価のために一般には堤防断面の二次元モデルに対する浸透流解析が行われる。このとき基礎地盤も含め浸透水の流下経路が堤外地から堤内地側へ「先細り」状である場合に浸潤線の上昇が顕著になり問題となるとされている1)。
しかし浸透経路の変化は堤体基礎地盤の三次元的な土質分布によっても影響を受ける可能性があると考え、その程度について三次元モデルによる浸透流解析を行い検討した。
2.解析方法
(1)堤体モデルと計算ケース区分
堤体を図1のような二次元形状でモデル化し、土質を堤体盛土、砂質土、粘性土の3種に単純に区分した。各土質の透水係数等は表1の値と仮定した。
三次元解析モデルは、上記の二次元の横断形状を河川の上・下流方向にそれぞれ80m引き伸ばした範囲で作成し、中央では同じ二次元断面であるが、基礎地盤の土質分布が堤防縦断方向に変化する形で設定した。解析メッシュを図2に示す。
計算ケースは図3に示したような4つのパターンを設定した。上・下流方向が対称のケースについては二分した片方のハーフモデルについて計算を行った。
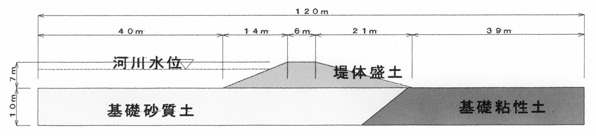
図1 二次元断面形状と土質区分
表1物性値一覧表
| 項目 土質 | 堤体盛土 | 基礎砂質土 | 基礎粘性土 |
|---|---|---|---|
| 飽和透水係数 | 1×10E-3cm/s | 1×10E-2cm/s | 1×10E-5cm/s |
| 有効間隙率 | 20% | 30% | 10% |
| 比貯留係数 | 1×10E-4/m | 1×10E-4/m | 1×10E-3/m |
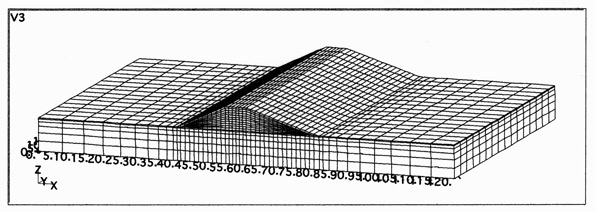
図2 解析メッシュ(ハーフモデル)
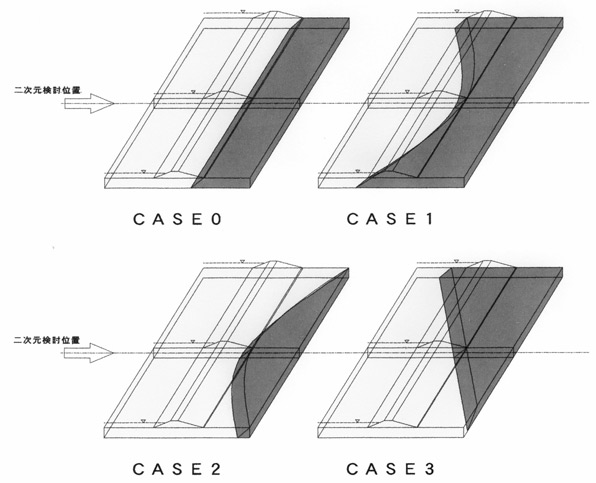
図3 土質分布の三次元モデルのケース分け
三次元解析モデルは、上記の二次元の横断形状を河川の上・下流方向にそれぞれ80m引き伸ばした範囲で作成し、中央では同じ二次元断面であるが、基礎地盤の土質分布が堤防縦断方向に変化する形で設定した。解析メッシュを図2に示す。
計算ケースは図3に示したような4つのパターンを設定した。上・下流方向が対称のケースについては二分した片方のハーフモデルについて計算を行った。
(2)計算条件
計算条件の設定においては文献2)3)を参考にした。
境界条件として河川側の表層には時間変化する河川水位に相当する水圧を与え、堤内側の端部は定圧境界、河川上下流端は不透水境界とした。降雨条件および河川水位の変化は図4のように与えた。初期状態で定常計算を行い、その後基本ステップを1時間として0〜120時間の非定常計算を行った。
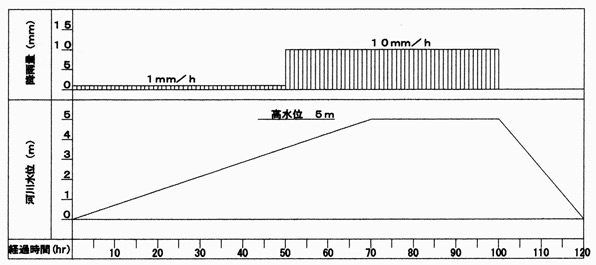
図4 降雨と河川水位変化の設定値
3.解析結果
ケース0のパターンは二次元解析と同じ結果を示すものであり、これと他のパターンとを比較した結果を整理する。
(1)浸潤線の差異
図5は中央断面位置における100時間目の地下水位(浸潤線)の位置を断面上にプロットした例である。ケース1では二次元に比べて若干高い水位となるが、差は小さい。ケース2では二次元よりもやや高い水位が得られており、断面位置の両側に分布する砂質土からの水圧の影響の可能性が考えられる。ケース3では二次元解析よりも低い水位となっており、透水性の良い砂質土が断面位置近くで分布が広くなるためと推定される。
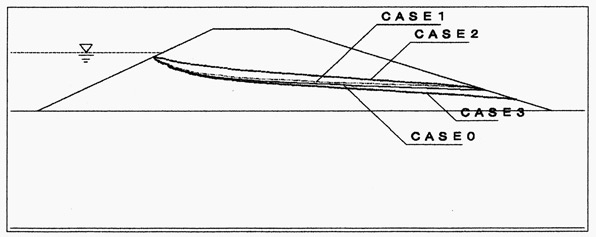
図5 浸潤線(水位)の違い(100時間目)
(2)水頭圧の経時変化
図6は堤防裏のり中央付近の底面位置の節点における圧力水頭の時間変化を抽出しプロットしたものである。ケースごとに水頭圧の上昇速度に差異が見られ、ケース2で水位の上昇がやや早く生じている。またピーク値にもケース間に差があることが読み取れる。
(3)縦断方向の地下水分布
縦断方向の水圧分布の形態をみるため、堤防裏のりで鉛直にカットした圧力水頭コンター図および堤防底面高さでの圧力水頭コンター平面図を図7、図8に示す。
いずれもケース1(ハーフモデル)の100時間目の計算結果の例である。土質分布の影響を受け境界付近で圧力水頭の分布形態が変化している状況が読み取れる。
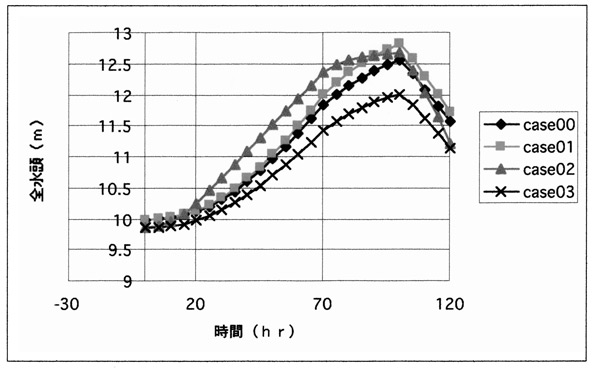
図6 圧力水頭の経時変化
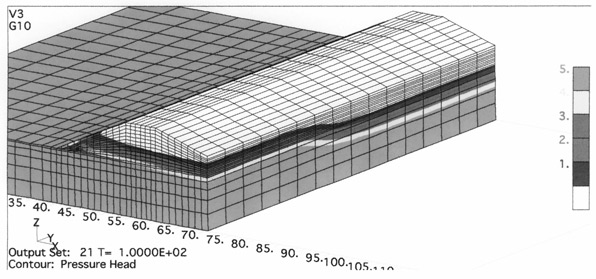
図7 圧力水頭鉛直断面コンター例
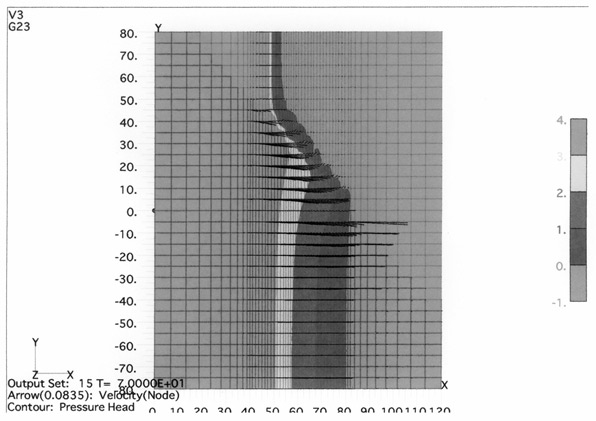
図8 堤体底面高さにおける圧力水頭平面コンター例
4.まとめ
限られたモデル解析による検討結果ではあるが、ある地点で二次元的には同じ堤防断面形態であっても、堤防縦断方向に基礎地盤の土質分布が変化する場合、二次元と三次元の浸透流解析では、結果が異なる場合があることが認められた。
このような水位・水圧の変化の差異は、基礎地盤の土質分布形状により発生することは明らかであり、三次元的に複雑な場所の浸透解析を二次元的な見方のみで検討した場合、異なる評価が得られる可能性が考えられる。
したがって堤防の耐浸透性の検討においては、旧河道の曲流部など、縦断方向の土質変化が予想される場合には、微地形判読や縦断方向の補完調査が重要であり、場合によっては三次元的な浸透流解析も必要になると考えられる。
《引用・参考文献》
- 土質工学会:建設計画と地形・地質、土質基礎工学ライブラリー26、pp.210〜217,1984
- 建設省河川局:河川堤防の浸透に対する調査要領,1997
- (財)国土技術研究センター:中小河川における堤防点検・対策の手引き(案),2004