1 .はじめに
小型動的貫入試験は、ハンマーの打撃が自動化された貫入試験である。この試験のよる試験値(Nd 値)は標準貫入試験値(N 値)との相関関係が良い試験である。今回は、Nd 値からの換算で求められるN 値との相関について、実際に標準貫入試験を実施した現場で、小型動的貫入試験を実施し、各土層毎の周面摩擦力の補正について検討した。
2.小型動的貫入試験の概要
3.検討事例
(1)調査ボーリング結果との相関
調査ボーリングを行った調査地において、ボーリング間の詳細な地層状態を把握する目的で小型動的貫入試験を実施した。調査ボーリングにおける標準貫入試験によって得られたN 値をもとに、層毎の平均N 値を求めた。平均N 値は層境界及び異質土の混入等の影響のない部分での平均を採用した。
また、同一敷地内で小型動的貫入試験を5 ~8 箇所実施し、ボーリングデータをもとに推測される地層断面及びNd 値をもとに、得られたNd 値を粘性土・砂質土・礫質土に区分し、前述の標準貫入試験のN値と比較した。
(2)N値から見るNd値
小型動的貫入試験より得られるNd値は1.(2)に示される換算式によってN値に置き換えられる。このとき、粘性土~礫質土における各土層毎の換算値を、準貫入試験のN 値と比較した。その結果、下表にまとめる値を得た。
表- 1 N値とNd値の比較(測定値)
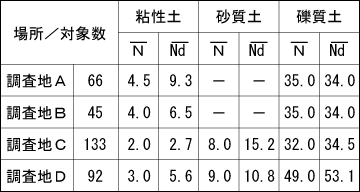
この結果より、礫質土層においては全般にN値とNd値の相関が良く現われていることが判る。逆に、粘性土においては、N値とNd値にややばらつきが見られる。 なお、これらの値は周面摩擦力を考慮し ないNd <10以下の値は省略して集計してある。
(3)周面摩擦力の補正係数
周面摩擦力は、貫入中の土層の影響を多大に受けるため、その貫入土層の差異によって周面摩擦力が異なるものと考えられる。よってここでは各土層において、標準貫入試験のN 値と良い相関が得られる周面摩擦力の補正係数を求めるものとする。
周面摩擦力の補正係数(β)は通常0.16 を使用しており、この値は全層に対して適用されている。しかしながら、上述のとおり、貫入中のロッドは各土層の周面摩擦力を抵抗として受けており、土層によってこの係数が異なることがあるのではないかと考えた。
そこで、標準貫入試験によって得られたN 値をもとに、小型動的貫入試験値Ndを換算する際の周面摩擦力補正係数(β)を逆算によって計算した。
(4)逆算による周面摩擦力補正係数(β)の算出
現在使われている式1 を用いて、周面摩擦力補正係数βを求める。
β={(Nd/2)- N }÷Mv ・・・式2
表-2 周面摩擦力補正係数β
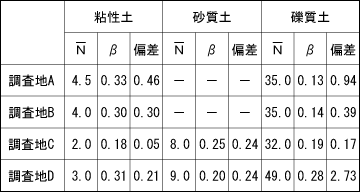
周面摩擦力補正係数βは、調査地A~C の礫質土層及び調査地Cの粘性土層においては現状の0.16 に近似した値を示し、誤差範囲が実測N 値と比較して小さいものと考えられる。一方、調査地A ・B ・D の粘性土層、調査地C ・D の砂質土層、調査地D の礫質土層においては現状の0.16 よりも大きい値を示し、実測値よりも大きい換算N 値を示すことが判明した。
(5)土層毎に対する周面摩擦力の補正
以上の結果より、各土層に対する周面摩擦力の補正係数βは以下のようになった。
〈粘性土〉
補正係数βは0.18~0.33 となった。調査地Cを除いては概ね0.31の値を得た。また、対象データは調査地A ・B ・D においては概ねGL-0~2m前後の表土層直下での値であった。また調査地CにおいてはGL-2~4m付近の値であった。深度における考察については次項(6)で述べる。
〈砂質土〉
補正係数は0.20~0.25 となった。調査地C 、Dでの平均は0.23の値を得た。なお、調査地A ・Bについては砂質土層の層厚が薄かったため、対象から除外した。対象データは粘性土層下位に分布する砂質土層であった。
〈礫質土〉
補正係数は0.13~0.28となった。各調査地の平均は0.18の値を得た。対象データはGL-2~5m前後の試験深度最下層であった。また、礫質土によく見られる礫当たりについては今回のデータから除外した。さらに、礫当たりで反発するもの以外にも、Nd 値が150 を越えるものについては同様に除外した。
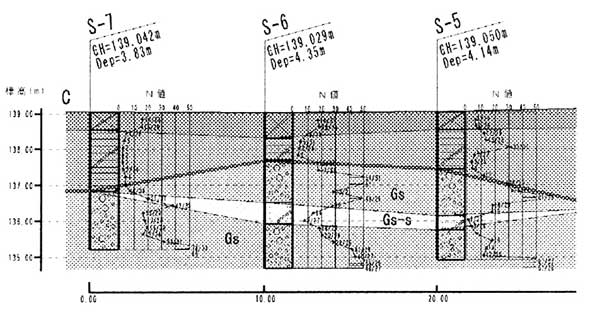
図- 2 小型動的貫入試験結果断面図
(6)深度における周面摩擦力の考慮
今回、検討対象とした地盤は上位に粘性土、中間層に砂質土、最下層に礫質土層が出現する堆積構造を示している。砂質土層・粘性土層においてはその上位に分布する土層の影響(摩擦力)を受けることが考えられる。今回の地層別補正では単純に各々の深度における周面摩擦力を考えたが、その中においても、調査地最上位(周面摩擦力を最も受けにくい地点)に分布する粘性土層で補正値にずれが見られた。このことは表層部以外の粘性土層において(調査地C )は、一般値(β=0.16 )に近似する値を得たのに対し、それ以外の調査地においてはβ=0.31の値を示し、上位のロッドの周面摩擦抵抗が加味されない場合においては、補正係数を変更する必要があるものと考えられる。
一般に、β=0.16の値はすべての土層に適応するように計算されているため、すべての条件に合致するとは言い難い面がある。今回の検討によって、特に表層部付近の粘性土層において、周面摩擦力の補正が必要であることが考えられる。
4.今後の課題等
今回、周面摩擦力の補正係数に対して表層部付近の粘性土は補正の対象となることを示したが、これ以外にも補正が必要な土層(堆積構造)を示す地点が出てくる可能性がある。また、今回は砂質土層でのデータ数がやや少なく、検討項目としては不十分だったため、砂質土層でのデータの採取も積極的に行いたい。比較対象のためにボーリング調査を行っている調査地での補足調査をこれからも行うとともに、可能な限りデータを採取し、より適正な条件付き補正係数の探求に努めたい。
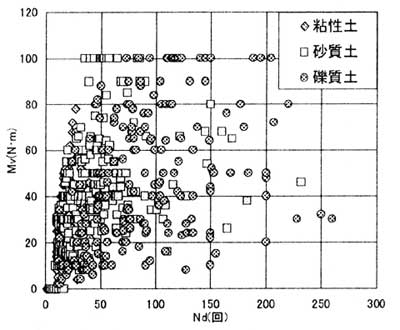
図- 3 Nd- Mv 相関図
また、今回検討した補正係数βは各土層の1 次関数によって得られた数値を採用したが、Nd 値との関係、深度との関係等により対数による評価等も今後検討していきたい。
《引用・参考文献》
1 )菅原紀明他:小型動的貫入試験機の開発とその利用、
2 )全地連「技術フォーラム'97 」講演集pp.461~464,1997.9.
3 )同「技術e- フォーラム2002 」講演集(CD- ROM)
小型動的貫入試験は、ハンマーの打撃が自動化された貫入試験である。この試験のよる試験値(Nd 値)は標準貫入試験値(N 値)との相関関係が良い試験である。今回は、Nd 値からの換算で求められるN 値との相関について、実際に標準貫入試験を実施した現場で、小型動的貫入試験を実施し、各土層毎の周面摩擦力の補正について検討した。
2.小型動的貫入試験の概要
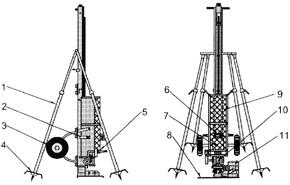
| (1)特 徴 小型動的貫入試験は、重さ30kgのハンマーを35cmの高さから自由落下させ、直径36.6㎜のコーンを地表より連続して貫入させることにより、地盤の硬軟及 び締まり具合を把握する試験である。この試験は地盤への貫入打撃回数が標準貫入試験(JIS-A-1219)の2倍となるように貫入力が設計されている。 (2)Nd 値のN 値への換算 小型動的貫入試験では、貫入ロッドにかかる周面摩擦力の影響で打撃回数が増加し、換算N 値を過大評価する恐れがある。そのため以下の式を用いて周面摩擦力の影響を取り除き換算N 値を算出する。なお、打撃回数が10 回未満の地盤については周面摩擦力の影響がないものとし、Mv=0 (N ・m )とする。 N ≒Ndm =α×Nd -β×Mv ・・・式1 |
 |
||||
| N:標準貫入試験値 Ndm:小型動的コーン貫入試験換算N 値 Nd:小型動的コーン貫入試験値 Mv:周面摩擦力(N・m ) α:打撃回数の補正係数(=0.5 ) β:周面摩擦力の補正係数(=0.16,Nd >10 ) |
|
||||
3.検討事例
(1)調査ボーリング結果との相関
調査ボーリングを行った調査地において、ボーリング間の詳細な地層状態を把握する目的で小型動的貫入試験を実施した。調査ボーリングにおける標準貫入試験によって得られたN 値をもとに、層毎の平均N 値を求めた。平均N 値は層境界及び異質土の混入等の影響のない部分での平均を採用した。
また、同一敷地内で小型動的貫入試験を5 ~8 箇所実施し、ボーリングデータをもとに推測される地層断面及びNd 値をもとに、得られたNd 値を粘性土・砂質土・礫質土に区分し、前述の標準貫入試験のN値と比較した。
(2)N値から見るNd値
小型動的貫入試験より得られるNd値は1.(2)に示される換算式によってN値に置き換えられる。このとき、粘性土~礫質土における各土層毎の換算値を、準貫入試験のN 値と比較した。その結果、下表にまとめる値を得た。
表- 1 N値とNd値の比較(測定値)

この結果より、礫質土層においては全般にN値とNd値の相関が良く現われていることが判る。逆に、粘性土においては、N値とNd値にややばらつきが見られる。 なお、これらの値は周面摩擦力を考慮し ないNd <10以下の値は省略して集計してある。
(3)周面摩擦力の補正係数
周面摩擦力は、貫入中の土層の影響を多大に受けるため、その貫入土層の差異によって周面摩擦力が異なるものと考えられる。よってここでは各土層において、標準貫入試験のN 値と良い相関が得られる周面摩擦力の補正係数を求めるものとする。
周面摩擦力の補正係数(β)は通常0.16 を使用しており、この値は全層に対して適用されている。しかしながら、上述のとおり、貫入中のロッドは各土層の周面摩擦力を抵抗として受けており、土層によってこの係数が異なることがあるのではないかと考えた。
そこで、標準貫入試験によって得られたN 値をもとに、小型動的貫入試験値Ndを換算する際の周面摩擦力補正係数(β)を逆算によって計算した。
(4)逆算による周面摩擦力補正係数(β)の算出
現在使われている式1 を用いて、周面摩擦力補正係数βを求める。
β={(Nd/2)- N }÷Mv ・・・式2
表-2 周面摩擦力補正係数β

周面摩擦力補正係数βは、調査地A~C の礫質土層及び調査地Cの粘性土層においては現状の0.16 に近似した値を示し、誤差範囲が実測N 値と比較して小さいものと考えられる。一方、調査地A ・B ・D の粘性土層、調査地C ・D の砂質土層、調査地D の礫質土層においては現状の0.16 よりも大きい値を示し、実測値よりも大きい換算N 値を示すことが判明した。
(5)土層毎に対する周面摩擦力の補正
以上の結果より、各土層に対する周面摩擦力の補正係数βは以下のようになった。
〈粘性土〉
補正係数βは0.18~0.33 となった。調査地Cを除いては概ね0.31の値を得た。また、対象データは調査地A ・B ・D においては概ねGL-0~2m前後の表土層直下での値であった。また調査地CにおいてはGL-2~4m付近の値であった。深度における考察については次項(6)で述べる。
〈砂質土〉
補正係数は0.20~0.25 となった。調査地C 、Dでの平均は0.23の値を得た。なお、調査地A ・Bについては砂質土層の層厚が薄かったため、対象から除外した。対象データは粘性土層下位に分布する砂質土層であった。
〈礫質土〉
補正係数は0.13~0.28となった。各調査地の平均は0.18の値を得た。対象データはGL-2~5m前後の試験深度最下層であった。また、礫質土によく見られる礫当たりについては今回のデータから除外した。さらに、礫当たりで反発するもの以外にも、Nd 値が150 を越えるものについては同様に除外した。

図- 2 小型動的貫入試験結果断面図
(6)深度における周面摩擦力の考慮
今回、検討対象とした地盤は上位に粘性土、中間層に砂質土、最下層に礫質土層が出現する堆積構造を示している。砂質土層・粘性土層においてはその上位に分布する土層の影響(摩擦力)を受けることが考えられる。今回の地層別補正では単純に各々の深度における周面摩擦力を考えたが、その中においても、調査地最上位(周面摩擦力を最も受けにくい地点)に分布する粘性土層で補正値にずれが見られた。このことは表層部以外の粘性土層において(調査地C )は、一般値(β=0.16 )に近似する値を得たのに対し、それ以外の調査地においてはβ=0.31の値を示し、上位のロッドの周面摩擦抵抗が加味されない場合においては、補正係数を変更する必要があるものと考えられる。
一般に、β=0.16の値はすべての土層に適応するように計算されているため、すべての条件に合致するとは言い難い面がある。今回の検討によって、特に表層部付近の粘性土層において、周面摩擦力の補正が必要であることが考えられる。
4.今後の課題等
今回、周面摩擦力の補正係数に対して表層部付近の粘性土は補正の対象となることを示したが、これ以外にも補正が必要な土層(堆積構造)を示す地点が出てくる可能性がある。また、今回は砂質土層でのデータ数がやや少なく、検討項目としては不十分だったため、砂質土層でのデータの採取も積極的に行いたい。比較対象のためにボーリング調査を行っている調査地での補足調査をこれからも行うとともに、可能な限りデータを採取し、より適正な条件付き補正係数の探求に努めたい。

図- 3 Nd- Mv 相関図
また、今回検討した補正係数βは各土層の1 次関数によって得られた数値を採用したが、Nd 値との関係、深度との関係等により対数による評価等も今後検討していきたい。
《引用・参考文献》
1 )菅原紀明他:小型動的貫入試験機の開発とその利用、
2 )全地連「技術フォーラム'97 」講演集pp.461~464,1997.9.
3 )同「技術e- フォーラム2002 」講演集(CD- ROM)