秋田大学教授 工学博士　　 及川 洋

04.土質・地盤工学における雑学的基礎知識
 平成15 年度地質調査技師登録更新講習会（盛岡会場）講演要旨

1 ．はじめに

　マイナス１ とマイナス１ を掛けるとプ ラス１ になる。また、任意の数にゼロを足したり、引いたり、掛けたりすることは許されるが、ゼロで割ることだけは許されない。これらの計算は日常生活では当然のこととして無意識に使用されている。しかし、マイナスとマイナスを掛けるとなぜプラスになるのか、また、なぜゼロで割ってはいけないのかなど、その理由を聞かれると、説明出来る人は意外と少ない。

　土質工学、地盤工学の中でも、無意識のうちに使用している基本的な計算式や概念、その他に、「なぜ」という素朴な質問が出た時、答えられない事象が意外と多い。ここではそのような幾つかの事例を取り挙げ、それらの答えを紹介する。なお、マイナスとマイナスを掛けるとプラスになる理由やゼロで割ってはいけない理由は本文の最後に示す。

2 ．「質量」と「重量」はなぜ区別しなければならないのか

　我々の体重は「質量」か「重量」かという区別に、理由を添えて即答できる人は意外と少ない。体重というからには重量と思っている人も多いと思われるが、体重の測定値は質量である。また、「何々の重量を量ってくれ」と人に頼むことが多いと思われるが、我々が「はかり」で量っている重さは質量であり、重量ではない。したがって本来は「何々の質量（または重さ）を量ってくれ」と頼まなければならない。

　このように、我々は質量と重量を明確に区別することなく、曖昧な状態で使用している。もちろん、日常生活には何ら不便は感じない。しかし、ＳＩ 単位の使用が義務づけられてきた昨今、技術者は質量と重量の違いを明確に区別できなければならない。いわゆる「馬」と「鹿」を明確に区別する必要がある。質量の単位はg （グラム）であり、重量の単位はN（ニュートン）であるが、これらは単に単位の違いだけではなく、前者はいわゆる「重さ」であり、後者は「力」であるという決定的な違いがある。以下に質量と重量の定義を簡単に復習しておく。

　物の重さを量る基準として国際度量衡局は、水温４ ℃の純水１cm 3 を標準分銅とした。そして、上皿天秤上でこれと釣り合う物体の重さを１ とし、これをその物体の「質量」と名付けた。また、その単位をg （グラム）とした。すなわち、標準分銅ｎ 個と釣り合う物体の質量（重さ）はｎg であり、標準分銅1,000 個と釣り合えば1,000g （=1kg ）となる。この天秤上での釣り合いは天秤を置く場所には関係しない。すなわち、物体が宙に浮いてしまう宇宙空間においても天秤のバランスは崩れない。したがって、質量は量る場所が変わっても値は変わらない。我々が日常使用している「はかり」はこの質量の値が表示されるように作られている。

　一方、物体の「重量」とは地球がその物体を引っ張ることによってその物体に発生している「力」であり、重さではない。このことは、重量の単位が力の単位N （ニュートン）であることからも明らかである。リンゴの実が木から落ちるのも、稲穂が垂れ下がるのも、全ては地球に物を引っ張る力（すなわち引力）があるためである。
一般に力はニュートンの第一法則により

力＝質量×加速度

として表される。この式は、質量1kg の物体に1m/s 2 の加速度が作用した時、その物体には1kg ･m/s 2 （=1N ）の「力」が発生することを示している。

　上記したように、地上の全ての物体は地球に引っ張られている。支えがなくなれば物体は落下する。落下の速度は約9.8m/s 2 の加速度をもつことも解っている。すなわち、地上の物体には常に約9.8m/s 2 の加速度（これを重力加速度という）が作用しており、支えがなくなれば約9.8m/s 2 の加速度をもって落下する。すなわち、地上の物体はその質量に重力加速度を掛けた大きさの「力」を常に持っている。我々はこの力を重量と呼び、次式でその値を算出している。

重量＝質量×重力加速度

　重力加速度は地球から離れるに従い小さくなり、宇宙空間でほぼゼロとなる。したがって、宇宙空間では物体は宙に浮くようになる。

　以上のように、質量は「重さ」（単位はグラム）であり、重量は「力」（単位はニュートン）である。

3 ．「有効応力」はなぜ「全応力」から「間隙水圧」を引くのか

　質量1g （1cm 3 ）の水の重さを水中で量るとその重さはいくらになるかがポイントとなる。水の重さを水中で量るような芸当は現実的にはできないが、水の重さを水中で量ると0g となる。これは、全ての物体は水中（正確には空気等も含めた流体中）では浮力を受けるためである。水自身も例外ではなく、水が水の中に入ると浮力を受ける。受ける浮力の大きさは水中に入った物体の体積に等しい水の重さである。すなわち、1cm 3 の水が水中に入ると1cm 3 分の水の重さ（1g ）の浮力を受ける。したがって、空中で1g の水が水中に入るとその重さは0g となる。空気が水中で浮くのはこの浮力があるためであることは言うまでもない。

　さて、本題に入り、体積V 、重量W の飽和した土を考える。前項で述べたように、この土の力はW である。いま、この土が水中に入ると、いわゆる地下水位以深にあると、土粒子はもちろんのこと、前述したように間隙水も浮力を受ける。受ける浮力の大きさは水の単位体積重量をγw とするとV ･γw である。したがって、この土が水中で発揮できる有効な力W 'は浮力の値を引いて

W '=W - V ･γw

となる。また、単位体積当りの力で表せば、

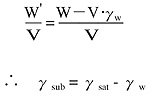となる。すなわち、水中での単位体積当りの有効な力はその物体が持っている本来の力から水による浮力を引かなければならないことが分かる。なお、γsub は水浸単位体積重量、γsat は飽和単位体積重量と呼ばれるもので、サフィックス[ sub]は「submarine ：潜水艦」、[ sat] は「saturation ：飽和」の略である

　力を応力に直すためには次の作業を行えばよい。すなわち、いま、この土が地下水面下Z の深さにあるとすれば、その面に働く応力は上式の両辺にZ を掛けて次式となる。

γsub ･Z =γsat ･Z- γw ･Z

　左辺のγsub ･Z は地下水面下Z の深さに働いている有効な応力（有効応力と記す。別名土粒子間応力とも呼ばれる）であり、右辺第１ 項目γsat ･Z は浮力が無いとした場合のその面に働く応力（全応力σ）、第２ 項目γw ･Z はその面の間隙水圧（u ）である。すなわち、

となり、有効応力は全応力から間隙水圧を引かなければならない。

4 ．なぜ雨が降ると地は固まるのか

　古くからのことわざに、「雨降って地固まる」という格言がある。一般に雨が降れば地盤は軟弱化するのが普通であり、両者の事象は相反する。しかるに、古人はなぜ、雨が降ると地は固まるという格言を残したのであろうか。この格言は古人達の体験が言葉になったものであるが、この体験の言葉は科学的には以下のように立証できる。

　すなわち、前述したように、地下水面下Z の深さにおける間隙水圧ｕ はu =γw ･Zであるが、実はこの値は水の動きがない場合の水圧（いわゆる静水圧）である。詳細は省略するが、水の動きがある場合には動水圧が加減され、一般には次式のように表される。

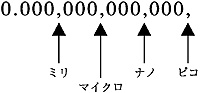
　ここに、i は動水勾配と呼ばれるもので、水の動きがある場合に値を持ち、水の動きが無い場合、すなわち静水圧の場合にはi=0 となる。

　符号の±は水が鉛直上向きに流れる場合にはプラスとなる。この場合、間隙水圧は通常より大きくなり、それに応じて有効応力は減少する。上向きの浸透水圧で砂地盤にパイピングやボイリングが起きるのはこのためであることは言うまでもない。

　一方、水が鉛直下向きに流れる場合の符号はマイナスとなる。この場合、間隙水圧は通常より小さくなり、有効応力は増大する。有効応力が増大すれば土は締まる。すなわち、鉛直下向きの水の流れは有効応力を増大させ、地盤を締める。以上は基本的には不飽和土内の水の流れにも適用される。その詳細も省略するが、鉛直下向きに流れる不飽和土内の雨水は土粒子に働く体積力を増大させ、地盤を締める。

5 ．鉄道駅の裏手はなぜ軟弱地盤地帯なのか

　あまり聞き慣れた言葉でないかも知れないが、昔の人は駅の裏は地盤が悪いと言う。確かにどの町においても駅裏の開発は近年のことであり、それまではあまり人も住んでいなかった。地盤が悪いためであり、人が住める状態ではなかったと言うのが正しい。なぜであろうか。

　東北本線が全線開通したのは今からちょうど110 年前の明治26 年（西暦1893 年）（東海道本線は明治22 年）である。当時の鉄道の動力源は石炭であり、列車は黒い煙と共に火の粉をまき散らしながら走った。一方、民家の屋根は殆どが茅葺きであった。すなわち、鉄道は火事の元であり、町の中を通す訳にはいかない。鉄道の誘致を拒否した町もあったほどである。このようなことから鉄道の駅は町はずれに造らざるを得ず、そこは大半が良好な地盤との境界地であった。

6 ．「ナノ」、「ピコ」スケールの概念はなぜ必要なのか

　環境保全の高まりにつれ、土質・地盤工学の分野においても、土壌汚染対策、地下水汚染対策が注目を集めている。汚染物質はその含有量が微量でも問題であり、その量は通常、ナノグラム、ピコグラム等のスケールで量られる。その意味で「ナノ」とか「ピコ」がどのような量であるかを実感として知っておく必要がある。これらは「力学」というよりはむしろ「化学」というイメージが強いが、実は土質・地盤工学の中にもナノスケールの力学は存在する。

　すなわち、一般廃棄物の最終処分場及び産業廃棄物の最終処分場に係る技術上の基準を定める省令（昭和52 年３ 月14 日総理府・厚生省令第一号）に、「不透水性地層が存在するか否かの判断は、厚さが５ メートル以上であり、かつ、透水係数が毎秒100 ナノメートル（岩盤にあってはルジオン値が１ ）以下である地層又はこれと同等以上の遮水の効力を有する地層が連続して存在しているか否かを調査して行うこと」という文面がある。透水係数と言えば我々は「十の何乗」という表現で表すことに訓練されており、100 ナノメートルと言われてもピンとこない。このスケールを実感するまでには相当の訓練が必要であるが、次のことを覚えればさほど難しくはないと思われる。

　すなわち、下記に示すように、小数点以下３ 桁目(10 - 3 ：千分の１)は「ミリ」、６ 桁目(10 - 6 ：百万分の１)は「マイクロまたはミクロン」、９ 桁目(10 - 9 ：十億分の１)は「ナノ」、12 桁目(10 - 12 ：一兆分の１)は「ピコ」である。「ミリ」、「マイ」、「ナノ」、「ピコ」の順に覚えればよい。

　ところで、毎秒100 ナノメートルとは10 - 5 cm/sec のことであるが、10 - 5 cm/sec という値も現実的にはピンとこない数値である。この数値は次のように単位を変換すると分かりやすい値となる。

10 - 5 cm/sec=6 ×10 - 4 cm/min
=3.6 ×10 - 3 cm/hour
=0.864cm/day
=3.15m/year

　10 - 5 cm/sec よりは3.15m/year の方が我々には分かり易い値である。しかるに、透水係数の単位をなぜcm/sec にしたのかが次の疑問となる。この答えは1856 年にダルシーが透水則を見出した時に使った材料が砂であったことから説明できる。

　いずれにしても、不透水層の目安となっている10 - 5 cm/sec という透水係数は、導水勾配が１ という条件のもとでは年間3.15m も水を通過させる値である。その層厚が5m あったとしても２ 年も経たない内に水は漏れてくる。このような値がなぜ不透水層の目安となったのかが次の「なぜ」という疑問である。

7 ．なぜ、マイナスとマイナスを掛けるとプラスになるのか

　答えは以下のとおり。

(- 1)(- 1)=(- 1)(- 1)+0
=(- 1)(- 1)+(+1)(1- 1)
=(- 1)(- 1)+(+1)(+1)+(+1)(- 1)
=(- 1)(- 1+1)+(+1)(+1)
=0+1=+1

８ ．なぜゼロで割ってはいけないのか

　 いま、A とB は等しい数とする。

A=B

両辺にA を掛ければ

A 2 =AB

両辺からB 2 を引けば

A 2 - B 2 =AB- B 2

両辺を因数分解すれば

(A+B)(A- B)=B(A- B)

両辺を(A- B)で割れば

(A+B)=B

A とB は等しいから

2B=B

∴ 2 ==1

となる。

　以上の計算はどこも間違ってはいない。しかし、１ と２ が等しくなっては数学的に困る。したがって、以上の計算のどこかを誤った計算作業とし、その作業を禁止せざるを得ない。禁止できるのは(A- B)=0 で割ることぐらいで、他の作業を禁止したら数学が全く成り立たなくなる。これが任意の数をゼロで割ってはいけないとした根拠である。
目次へ戻る